以下内容主要引用自《Deep Learning》中文版

 

1、线性方程组以矩阵的形式表达如下，

　　　　　　　　　　　　　　

其中是一个已知矩阵，也就是一个m行n列的矩阵；

是一个已知向量（m行1列）；

是一个我们要求解的未知向量（n行1列）。

 

矩阵A中的每一个行和b中对应的元素构成一个约束，所以线性方程可以换种表达方式：

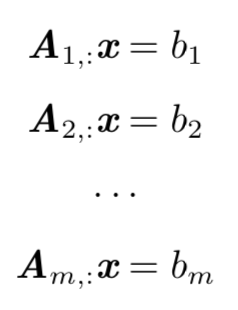 　　　　　　　　　　　　　　， 用A的每一行和x向量相乘得到b向量的一个元素 

 

　　　　　　　　或者详细的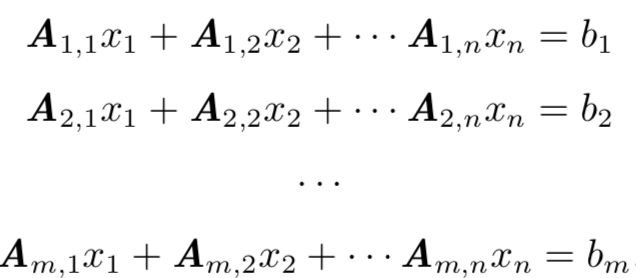：， 这也是一般多项式的表达。

 

2、通过逆矩阵，我们可以求得线性多项式的解。

逆矩阵的性质：矩阵和其逆矩阵相乘等于单位矩阵。

 　　　　　　　　　　　　　　

逆矩阵求解多项式的推导过程：也就是逆矩阵左乘的过程。

 　　　　　　　　　　　　

 

3、如果逆矩阵存在，那么对于每一个向量b恰好存在一个解。

4、从方程组考虑，对于b的某些值，解的情况只会有三种可能：

• 只存在一个解（只限于方阵，存在逆矩阵）
• 不存在解
• 存在无限多个解

　 不存在多于一个解，少于无限个解的情况： 假设x和y都是方程组的解，考虑下面等式，α是任意值，z也是方程组的解。

 　　　　　　　　　　　　　　

5、线性方程组也可以换一种理解角度：

• 可以将A的列向量看作从原点出发的不同方向，分析有多少个解的过程，也就是确定有多少种方法可以到达向量b，也就是坐标系中从原点到b点的路径。
• 解向量x中的每个元素表示的是沿着对应的A的列向量的方向走多远。

 　　　　　　　　　　　　　　　

     这种操作就是线性组合。一组向量的线性组合，是指每个向量乘以对应标量系数之后的和。

 

生成子空间（span）：原始向量线性组合后所能抵达的点的集合。

列空间（值域）：确定Ax=b是否有解，相当于确定向量b是否在A的列向量的生成子空间中。

• 如果对于任意b ∈ R^m，Ax=b都有解，那么A的列空间需要构成整个R^m。
• 如果R^m中的某个点不在A的列空间中，那么该点对应的b无解。
• A至少m列

 

6、线性相关和线性无关

线性无关：一组向量中的任意一个向量，都不能表示成其他向量的线性组合。

线性相关，反之。

• 线性相关的向量加入向量组中，不会增加向量组的生成子空间。
• 如果A的列空间构成整个R^m，那么A必须包含至少一组m个线性无关向量。
• 以上是对每一个b取值都有解的的充要条件。